Los matemáticos de la RUDN han demostrado un teorema que ayudará a calcular el movimiento del agua en rocas porosas

Los matemáticos de la RUDN han demostrado el teorema de unicidad para la continuación de una solución unidimensional a un problema de difusión de orden fraccionario. Tales ecuaciones surgen, por ejemplo, en problemas de propagación de un fluido en un medio poroso, por ejemplo, filtración de agua subterránea. Los resultados de los matemáticos de la RUDN son necesarios para un análisis más preciso de las soluciones y su simulación numérica. En el caso general, estos teoremas de extensión para otras clases de ecuaciones similares son desconocidos. El artículo fue publicado en la revista Fractional Calculus and Applied Analysis.

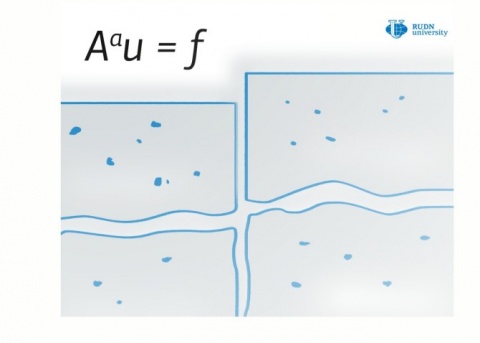
La ecuación de difusión es una ecuación diferencial parcial que describe la penetración de un fluido en un medio. Su solución es una función de u como una función de t y x, que da la concentración de fluido en el punto x en el tiempo t. La ecuación de difusión unidimensional contiene derivadas de u con respecto a t, así como derivadas de u con respecto a x y una segunda derivada de u con respecto a x. La ecuación unidimensional también se llama ecuación de calor: la propagación de calor puede considerarse como una forma de difusión. En la ecuación de difusión fraccionaria unidimensional, la derivada de u con respecto a t se reemplaza por la derivada fraccionaria de Caputo. Si la derivada es el límite de alguna relación, entonces la derivada fraccionaria de Caputo de un orden fraccionario a está dada por la fórmula integral, donde para valores enteros a hay valores estándar de las derivadas. Para la ecuación de difusión unidimensional habitual, existe un teorema de continuación. Dice que si la densidad y el flujo de partículas son cero en un punto límite durante un intervalo de tiempo, entonces no hay difusión en x y t bajo consideración. La prueba de esta afirmación está dentro del poder de un estudiante de primer año, sin embargo, hasta hace poco, tales resultados no se conocían para la ecuación de difusión fraccionaria.

El matemático de la RUDN Masahiro Yamamoto y sus colegas consideraban la ecuación de difusión fraccionaria unidimensional para un parámetro arbitrario a entre 0 y 1. Lograron demostrar que en el caso fraccionario también existe un teorema de continuación y además y en la misma formulación: si la densidad y el flujo de partículas son cero en un punto límite durante un intervalo de tiempo, entonces nada se difunde.

(Foto: RUDN)

La idea de la prueba es la siguiente: los matemáticos toman una solución, observan su comportamiento en una continuación y luego obtienen una estimación integral del crecimiento de esta solución, según el parámetro. De la estimación integral se deduce que la única solución que la satisface es la solución cero. Para ecuaciones similares con derivados fraccionarios, actualmente no se conocen tales estimaciones.

La ecuación de difusión fraccionaria se aplicará en varios campos de la física, las matemáticas y la informática. Por ejemplo, esta ecuación describe la propagación de un fluido en un medio poroso. Dichas ecuaciones se han utilizado con éxito para describir las emisiones de contaminación en las aguas subterráneas. Otra área de aplicación de tales ecuaciones es el procesamiento de imágenes. (Fuente: RUDN)