Se describen los frentes de onda de una ecuación que describe la difusión de los virus en los tejidos

El matemático de la universidad RUDN (Rusia) estableció las propiedades de frentes de onda en los sistemas de reacción–difusión. Los datos obtenidos ayudarán a hacer el seguimiento de la propagación de los virus en los tejidos y pronosticar el estado de ecosistemas. El artículo fue publicado en Nonlinearity.

Los modelos de reacción–difusión son generalizaciones de la ecuación de difusión de Fick que describen la concentración de sustancia en el medio como una función que depende de la coordenada y tiempo. A su vez, la velocidad de cambio de la concentración de la sustancia es proporcional a la segunda derivada de la concentración en la coordenada. Las ecuaciones de reacción–difusión describen las concentraciones de algunas sustancias en la solución que no solamente se difunden, sino reaccionan entre ellas químicamente. Matemáticamente estas ecuaciones se distinguen de las ecuaciones de Fick ya que contienen un miembro adicional que describe el cambio de las concentraciones por las reacciones químicas. Este miembro depende no linealmente de la concentración, precisamente por eso estos modelos son de un gran interés y de gran dificultad para el estudio.

Uno de los tipos de modelos de reacción–difusión son los sistemas con retardo donde el miembro no lineal (velocidad de reacción) depende no solamente de una función desconocida en el momento de tiempo, sino también de su valor de hace un tiempo atrás. Estos sistemas son necesarios, por ejemplo, en el campo de la ecología matemática: el retardo en ecuaciones es justamente el período de crecimiento de la especie, tiempo cuando el animal no participa en la reproducción y no influye en el aumento de la población. Problemas semejantes aparecen y en teoría del control, donde a menudo aparecen sistemas que reaccionan con retraso al impacto. De la misma manera, los resultados obtenidos pueden ser aplicados a la modelación matemática en biomedicina.

(Foto: RUDN)

El matemático de RUDN Vitaliy Volpert junto con su colega chileno analizaron una variación de la ecuación de reacción-difusión con retardo que no había sido investigada anteriormente.

En los trabajos anteriores de científicos extranjeros se examinaron modelos que estan limitados por la monotonía en el miembro de reacción, lo cual limitaba su aplicación a los nuevos problemas de la biología y ecología matemáticas. En el nuevo trabajo, al contrario, fueron examinadas dos de las más complicadas variaciones de la ecuación de reacción-difusión.

En este trabajo fue demostrada la existencia de soluciones con los frentes de onda monótonos para una variante particular de ecuaciones de reacción-difusión biestables. El significado físico de tales procesos se explica de la siguiente manera: el sistema tiene dos estados estables y el frente de onda se difunde de un equilibrio estable hacia el otro.

En el nuevo trabajo los matemáticos descubrieron que dependiendo de la velocidad de la onda se cumple uno de los dos escenarios de desarrollos de los frentes de onda. En el primer caso, las ondas son siempre monótonas, mientras que en el segundo comienzan a oscilar bajo grandes retrasos. 

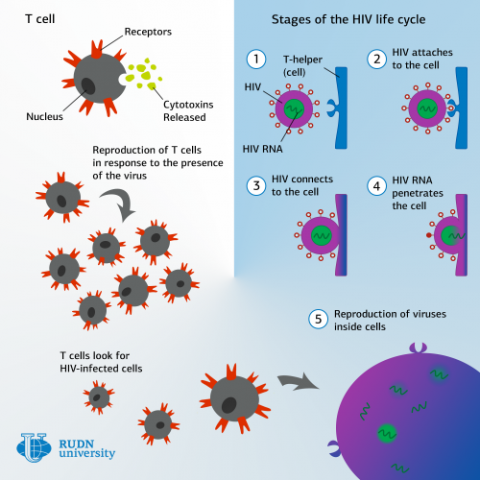
Los resultados obtenidos permiten implementar los sistemas de reacción-difusión en nuevos problemas aplicados. Por ejemplo, ahora los científicos podrán simular matemáticamente la propagación de los virus en los tejidos. Esto permitirá responder las preguntas sobre cómo el estado de enfermedad depende de la carga viral inicial y de la velocidad e intensidad de la respuesta del sistema inmune. En la práctica, esto permitirá mejorar la precisión de los exámenes que detectan enfermedades crónicas.

Además, los nuevos resultados permiten tener en cuenta el efecto de Allee, que es la relación entre las dimensiones de la población y la velocidad de su reproducción. Ayudará a la industria a optimizar los criaderos de peces y salvar las especies en peligro de extinción. En general, los descubrimientos científicos en este sector tienen una multitud de aplicaciones no solamente para la biología y ecología matemáticas, sino para los problemas de la cinética química y teoría del control. (Fuente: RUDN)